Sur la mesure du cercle et
de la sphère en Égypte ancienne
Kossivi
ADJAMAGBO
- Cheikh M'Backé DIOP
Article publié dans
ANKH n°4/5
"La circonférence
est fière
D'être égale à 2pR,
Et le cercle est tout joyeux
D'être égal à
pR2
Le volume de la sphère
Quoi que l'on puisse faire,
Est égal à 4/3pR3
La sphère fût-elle de bois"
Marcel PAGNOL
Éléments d'une
thermodynamique nouvelle
Résumé
: Dans le présent article sont
commentés deux problèmes mathématiques traités dans deux papyrus
égyptiens : le calcul de l'aire d'un cercle (Papyrus Rhind) et le calcul
de la surface d'une demi-sphère (Papyrus de Moscou). Ces calculs
constituent la première formulation connue, dans l'histoire universelle
des mathématiques, des problèmes suivants : la quadrature du cercle,
la rectification de la circonférence et l'aplanissement d'une
surface courbe. Nous montrons l'importance du rôle joué par la
notion de mesure dans l'établissement des formules égyptiennes. L'examen
des formules mathématiques égyptiennes révèle à la fois une démarche
théorique implicite et la mise au point de techniques algorithmiques et
numériques efficientes pour résoudre des problèmes concrets.
Abstract
:
On Measure of Circle
and Sphere in Ancient Egypt
—
In the present article are commented two
mathematical problems treated in two Egyptian papyri : the calculation
of the surface of a circle (Papyrus Rhind) and the calculation of the
surface of a hemisphere (Moscow Papyrus). These calculations are the
first known formulation, in the Universal History of Mathematics, of the
following problems : the quadrature of the circle, the staightening of the circumference and the
levelling of a curved
surface. The important role of the notion of measure in the Egyptian
formula is also shown. The study of the Egyptian mathematical formula
reveals an implicit theorical thought process as well as the building of
algorithmic and numerical efficient techniques in order to solve
concrete problem.
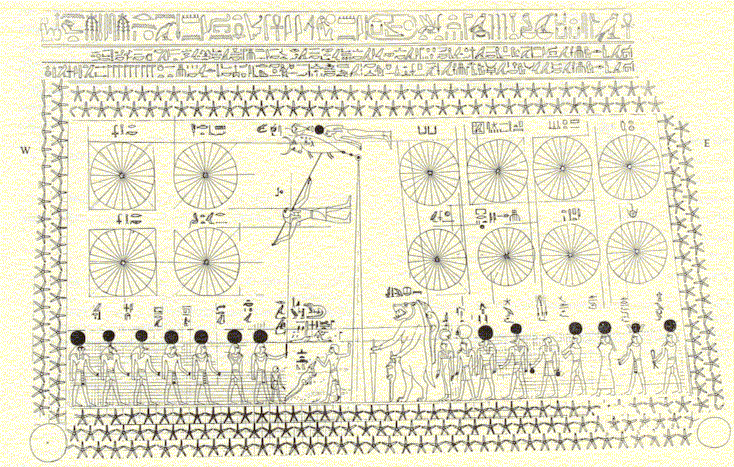
Figure 1 : Plafond
astronomique de la tombe de SENENMUT (vers 1500 av. J.C.). SENENMUT
était l'architecte du temple de la reine HATSHEPSUT (Deir el Bahari). On
note la discrétisation des cercles en 24 secteurs égaux.
1. Introduction
Nous
proposons un commentaire de deux problèmes mathématiques posés et
résolus par les anciens Égyptiens : le calcul de la surface du cercle,
traité dans les Problèmes n°48 et 50 du Papyrus Rhind, et le
calcul de la surface de la demi-sphère, traité dans le Problème n°10
du Papyrus de Moscou. Ces deux problèmes renvoient immédiatement à
trois autres problèmes qui apparaissent implicitement formulés pour la
première fois dans l'histoire universelle des mathématiques (environ
1500 ans av. J.-C.) : la quadrature du cercle, la rectification de la
circonférence, l'aplanissement d'une surface courbe.
Les papyrus pré-cités ont
fait l'objet de nombreuses études approfondies. Notre but est de
répondre aux deux questions suivantes qui n'ont pas reçu, à notre sens,
de réponses suffisamment satisfaisantes :
— Existe-il dans les
documents laissés par les Égyptiens anciens des éléments permettant
d'expliquer le caractère exact et général des formules mathématiques
qu'ils ont élaborées et utilisées, en particulier celles concernant la
surface du cercle et la surface de la demi-sphère ?
— Est-il possible de
restituer ces formules mathématiques par une démonstration qui
respecterait le niveau de connaissance tel qu'il est suggéré par les
documents connus à ce jour ?
Les études consacrées aux
mathématiques égyptiennes font apparaître deux approches différentes :
— la première, sous-jacente
aux travaux de E. T. PEET, postule le caractère empirique du savoir
mathématique égyptien. Ce point de vue est très souvent repris dans des
ouvrages de vulgarisation d'une haute tenue : "Mais leur plus grand
titre de gloire, en géométrie plane, est la possession d'une recette
pour calculer la surface d'un cercle en fonction de la longueur de son
diamètre" (G. POSENER, sous la direction de, Dictionnaire de la
civilisation égyptienne, Paris, Fernand Hazan, 1970, p. 165), "Elle
ne se soucie pas de démonstrations, mais donne des "recettes" plus ou
moins approximatives" (André PICHOT, La naissance de la science,
tome 1. Mésopotamie, Égypte, Paris, Gallimard, 1991). Cette démarche
conduit à rechercher les procédures empiriques (qui s'opposeraient à une
approche théorique abstraite) par lesquelles les anciens Égyptiens
auraient abouti à leurs résultats.
— la seconde attire
l'attention sur des faits qui excluent un simple empirisme, et qui
expriment de manière implicite ou explicite la connaissance de
propriétés mathématiques et l'existence d'une réflexion théorique sur
des êtres mathématiques. C'est le cas des auteurs comme V. V. STRUVE en
Allemagne, R. J. GILLINGS aux USA, C. A. DIOP et
T. OBENGA en Afrique,
S. COUCHOUD en France.
Suivant cette dernière
approche nous nous proposons, en premier lieu, de rappeler que le
mathématicien égyptien a introduit les notions de discrétisation (ou
pavage) et d'unité qui renvoient au concept mathématique fondamental de
mesure. C'est justement ce concept de mesure qui permet d'expliquer,
selon nous, à la fois l'exactitude et le caractère général des formules
mathématiques produites par les Égyptiens et que ceux-ci ont utilisées
pour résoudre des problèmes pratiques.
Le niveau des connaissances
mathématiques révélé par les textes égyptiens est incompatible avec
l'idée qui consiste à considérer les formules mathématiques égyptiennes,
pourtant exactes (par exemple la formule du volume du tronc de pyramide,
cf. Problème n°14 du Papyrus de Moscou), comme de simples
recettes. Nous montrerons a contrario qu'il est possible de
proposer une démonstration mathématique rigoureuse de la formule de la
surface du cercle et de celle de la surface de la demi-sphère tout à
fait compatible avec le niveau de connaissances attesté par les
documents égyptiens disponibles.
Notre analyse soulignera
l'originalité des solutions apportées par le mathématicien égyptien qui
a su ramener le calcul de la surface d'un cercle à celle d'un carré et
celle d'une demi-sphère à la surface d'un rectangle.
2. Aux
origines de la notion mathématique de mesure en Afrique
En
Afrique, la vallée du Nil abrite parmi les plus anciennes attestations
de la mesure d'une grandeur. Citons :
— La mesure du temps
; elle est effectuée d'une part en utilisant des calendriers, et d'autre
part à l'aide d'horloges à eau (clepsydre), d'horloges à ombre et
de cadrans solaires. Les trois calendriers lunaire, solaire (de 365
jours, ancêtre direct du calendrier actuel) et sidéral ou astronomique
(d'une périodicité de 1460 ans, durée séparant deux levers héliaques de
l'étoile Sirius) sont déjà en vigueur à l'Ancien Empire égyptien
c'est-à-dire au IIIe millénaire av. J.-C..

Le calendrier d'Eléphantine
- 1450 av. J.C. (Musée du Louvre)
La clepsydre est en usage au
Nouvel Empire comme en témoigne celle provenant du Temple de Karnak (Thèbes-Est)
et datant de la fin de la XVIIIe dynastie sous le règne du
pharaon Aménophis III (1408-1372 av. notre ère).

Clepsydre
(Karnak, 1400 av. J.C.)
— La pesée ;
l'invention de la balance et des poids associés, attestés dès le
prédynastique, (fin du IVe millénaire av. J.-C.) permet de procéder en
particulier à la pesée de l'or.

Poids
trouvés à Uronarti au Soudan - XIIeme dynastie 1991-1786 av.
J.C. (Museum of Fine Arts, Boston). Remarquer les inscriptions
hiéroglyphiques.
Tombe de
Nebamon - 1400 av. J.C.
— La mesure d'une
longueur et d'une surface ; la configuration géographique
particulière de la vallée du Nil et le régime des crues du fleuve qui
effaçait les délimitations des champs président à la naissance de la géométrie (étymologiquement : "la mesure de la terre"). Ainsi,
l'invention de la chaîne d'arpentage et de la règle permet d'effectuer
des mesures de longueur.
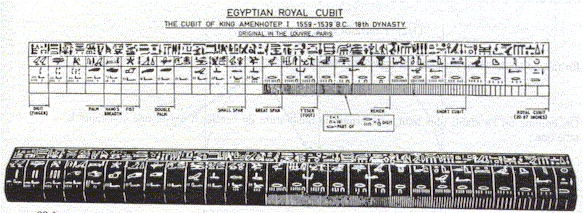
Dessin de la
coudée royale égyptienne attribuée à Aménophis Ier (1559-1538 B.C.,
18e dynasrie). L'original se trouve au Musée du Louvre. (cf. R. J.
GILLINGS, op. cit., p. 220). Les Égyptiens ont défini le "double
remen" comme unité de longueur qui est égale à la diagonale d'un
carré dont le côté a pour longueur la coudée royale : 52,3 cm.

Relief
provenant d'Amarna (Brooklyn Museum 665.16. Charles Edwin Wilbour
Fund) montrant un terrain divisé en parcelles carrées. Reproduit par
T. OBENGA dansThéophile OBENGA, La Géométrie égyptienne -
Contribution de l'Afrique antique à la Mathématique mondiale, Paris,
L'Harmattan/Khepera, 1995, p. 51.
— La mesure d'un
volume ; elle est nécessaire à l'économie et à l'édification d'une
architecture monumentale parfaitement maîtrisée4...
Les papyrus (Papyrus
Rhind, Papyrus de Moscou, Papyrus de Kahun), les
instruments de mesures (règles, balances, chaînes d'arpentages,
horloges, etc.) et les monuments décorés que nous a légués l'Égypte
ancienne montrent que les deux notions fondamentales de discrétisation et d'unité de mesure sont
clairement appréhendées par l'Égyptien. Ces deux notions, liées entre
elles, sont en effet indispensables pour établir des formules générales
exactes.
Illustrons cette assertion
par l'exemple suivant. Considérons un rectangle quelconque dont on
cherche à déterminer la surface notée S. Effectuons une
discrétisation de la surface du rectangle considéré en carrés
élémentaires de même surface notée s. Cette opération de
discrétisation conduit à décomposer la surface S du rectangle en
m rangées de n carrés de surface s. On a donc :
S = nxmxs
Si l'on introduit l'unité de
longueur à partir de la surface unité s, on a :
S = (nxs1/2)x(
mxs1/2)=
axb
où a et
b sont
respectivement la longueur et la largeur du rectangle.
On comprend, sur cet
exemple apparemment simple, que S = axb
constitue une formule générale dès lors que a et b sont
mesurées avec la même unité .
Or, les documents que nous
possédons montrent qu'existaient, en Égypte ancienne :
a)
une définition
cohérente de la coudée, mh, comme unité de
mesure de longueur (52,8 cm ; Problèmes 56 et 59 du Papyrus Rhind) et de la
coudée carrée comme unité de
mesure de surface (Problèmes 7 et 17 du Papyrus de
Moscou) ainsi que la coudée cubique comme unité de volume (Problèmes
41 et 47 du Papyrus Rhind, Papyrus de Kahun).
Ce fait est très
important car il montre que le mathématicien égyptien avait généralisé
la notion de mesure d'un espace à une dimension à un espace à trois
dimensions à partir de la même unité de base : la coudée.
Ainsi, le caractère général et exact des formules mathématiques établies
par les Égyptiens dans le domaine de la géométrie perd une partie de son
mystère si l'on observe qu'ils ont introduit la notion mathématique de
mesure, traduite par la définition d'un système d'unité cohérent lorsque
l'on passe de la mesure d'une longueur (problème à une dimension) à
celle d'une surface (problème à deux dimensions) puis à celle d'un
volume (problème à trois dimensions). C'est ce qu'illustre l'exemple du
calcul de la surface du rectangle présenté plus haut. T. OBENGA
écrit avec pertinence : "En Égypte, l'unité de surface est la surface
d'un carré qui a pour côté l'unité de longueur. En Babylonie, l'unité de
surface (mus/sharum, environ 36 m2)
n'est pas la surface d'un carré qui a pour côté l'unité de longueur (amatum,
"coudée", environ 50 cm)".
Dans la pratique l'unité de
longueur était le khet ("verge"), qui valait 100 coudées et
l'unité de surface le setat qui valait 100 coudées
carrées, dénommé aoure, par les Grecs (Problèmes 56 et 59 du
Papyrus Rhind). La coudée cube comme
unité de mesure de volume est convertie dans des unités plus aisées à
manipuler (khar, hekat).
b) un
vocabulaire désignant des êtres mathématiques et leurs éléments
caratéristiques (nombre, mesure, cercle, sphère, cylindre, diamètre,
surface, circonférence, rayon, section plane ou grand cercle, de la
sphère, carré, rectangle, largeur, longueur, triangle, hauteur, base,
sommet, angle, volume, pyramide, apothème, etc.)5.
Les mots utilisés sont tirés du vocabulaire courant dont le champ
sémantique s'est étendu à des notions abstraites comme c'est le cas dans
les langues parlées aujourd'hui : par exemple, les termes de clan,
tribu et de pavé en Théorie de la mesure et de
l'Intégration, l'une des plus abstraites en mathématique, celui
de voisinage en Topologie ou encore le terme de champ en
physique (la théorie quantique des champs), le mot théorie qui,
étymologiquement en grec, signifie contemplation.
c) des
formules exactes et générales de calcul de surface et de volume
(entre autres) : témoins, les Problèmes du Papyrus Rhind, les Problèmes de Papyrus de Moscou. Bien avant PLATON
les Égyptiens ont conçu des formes géométriques idéales, abstraites, des êtres mathématiques (cercle, carré, rectangle,
sphère, ellipse, triangle, trapèze, cylindre, pyramide, etc.) que l'on
ne rencontre pas dans la nature et dont ils ont découvert qu'elles
avaient des propriétés générales utilisables pour résoudre des problèmes
concrets d'ordre agricole, économique, architectural ... Ces formules
supposent une définition implicite de la longueur et de la surface d'un
cercle, de la surface d'une sphère, etc., définitions qui sont également
restées implicites chez ARCHIMÈDE
qui les utilisait.

Problèmes du Papyrus Rhind
(British Museum)
d)
des techniques
de discrétisation (ou pavage) de surfaces en carrés, secteurs
triangulaires, ou encore trapèzes élémentaires (cf. le Problème n° 48
du Papyrus Rhind, voir aussi les figures reproduites dans cet
article : Le plafond astronomique de la tombe de SENENMUT
(vers 1500 av. J.C.) ; SENENMUT
était l'architecte du temple (Deir el Bahari) de la reine HATSHEPSUT
; le bas-relief provenant
d'Amarna montrant un jardin divisé en lots carrés ; la méthode de
quadrillage mise en œuvre pour réaliser les dessins ; ostracon calcaire,
montrant la discrétisation le long d'une ligne courbe, datant du IIIe
millénaire av. J.-C.).
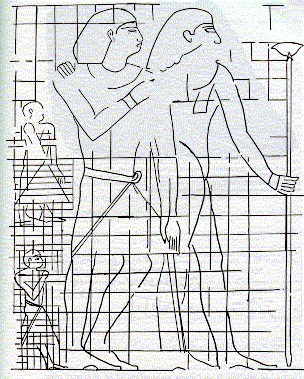
Figure 4
: La
méthode des carreaux pour réduire ou agrandir un dessin. BLACKMAN,
The Rock Tombs of Meir, II, pl. II, reproduit par T. OBENGA
dansThéophile OBENGA, La Géométrie égyptienne - Contribution de
l'Afrique antique à la Mathématique mondiale, Paris, L'Harmattan/Khepera,
1995, p. 69.
e) les notions de
proportionnalité et d'homothétie : la méthode des carreaux inventée
pour réduire ou bien agrandir un dessin (voir figure), le "théorème de THALÈS"
était connu des Égyptiens qui l'ont justement enseigné à THALÈS
(cf. PLUTARQUE, Le
Banquet des Sept Sages, cité par T. OBENGA
; Problème n° 53 du Papyrus Rhind).
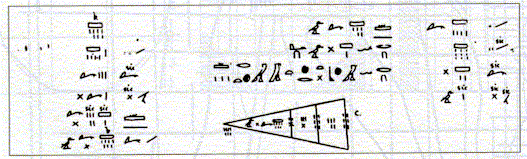
Figure 6 :
Le problème 53 du Papyrus mathématique Rhind. T. E. PEET : The
Rhind Mathematical Papyrus, pl. P. Le Papyrus Rhind est une recopie
par le scribe Ahmès (vers 1650 av. J.-C.) d'un texte datant du Moyen
Empire (2040-1785 av. J.-C.). La reproduction ci-dessus est une
transcription sous forme hiéroglyphique du texte hiératique (cf. photo
de couverture). Le problème 53 traite de l'aire du trapèze ; Il suppose
la connaissance du théorème dit de THALÈS.
Ceci signifie que l'Égyptien
a su construire une mesure au sens mathématique et l'appliquer avec
succès pour déterminer aires et volumes divers à l'aide de formules
mathématiques générales établies par lui et formellement exactes.
Ainsi, la méthode de
discrétisation (ou pavage) inaugurée par l'Égypte ancienne conjuguée à
la notion d'unité de mesure apparaît dans une perspective historique
comme l'ancêtre lointain des Sommes de DARBOUX,
de l'Intégrale de RIEMANN,
de la Méthode des trapèzes utilisée pour intégrer une fonction.
Si, bien évidemment, les
mathématiques ont fait des progrès immenses depuis l'Antiquité, le
concept même de mesure attendra le XIXe siècle pour connaître une
mutation profonde au sens mathématique.
En effet, à la fin du
XIXe siècle, le mathématicien français LEBESGUE
généralise la notion de mesure : la mesure de LEBESGUE
est définie sur un ensemble plus général que
l'ensemble des intervalles de Rn
(R désigne l'ensemble des nombres réels) et que l'on appelle la
tribu borélienne de Rn.
La mesure de LEBESGUE
sera elle-même généralisée, conduisant aux
distributions qui jouent un rôle fondamental pour réaliser des
mesures relatives à des phénomènes stochastiques.
Signalons enfin
l'introduction de nouvelles mesures comme la mesure fractale (PONTRJARGIN
et SCHNIRELMAN, 1932 ; MANDELBROT,
1982), qui viennentt encore enrichir le concept de mesure.
3. La
quadrature du cercle
Le
Problème n°48 du Papyrus Rhind pose pour la première fois dans
l'histoire des mathématiques la problématique de la quadrature du
cercle : il s'agit de comparer la surface d'un carré de 9 unités de
côté à celle du cercle inscrit de diamètre 9 unités.
Si l'on suit les
diagrammes proposés par VOGEL
et GILLINGS
(cf. figures 2 et 3) on voit que la réponse que les Égyptiens y
apportent repose sur la notion de mesure construite à partir des deux
notions de discrétisation et d'unité évoquées au précédent paragraphe.
En effet, la surface du cercle est recherchée comme la surface d'un
carré unique équivalent à une somme de carrés élémentaires unitaires et
fractionnaires recouvrant au mieux la surface du cercle :
Cette opération de la mesure
du cercle par quadrature peut être considérée, en quelque sorte, comme
l'opération inverse de la mesure du cercle par discrétisation : c'est le
retour à l'un après transformation de l'un en le multiple. C'est le
retour à l'un – le carré – après fractionnement de l'un – le cercle – en
une multitude d'éléments, ce qui illustre la dialectique de l'un et du
multiple.
L'intérêt des
diagrammes de VOGEL et GILLINGS
est qu'ils offrent une explication plausible pour l'obtention de la
valeur égyptienne du nombre
p.
Cependant ils ne répondent pas à la question concernant l'obtention de
la formule égyptienne donnant l'aire du cercle et considérée sous
l'angle de sa généralité.
Notre commentaire aborde
cette problématique de la quadrature du cercle sous ses deux aspects
distincts : le résultat mathématique que constitue la formule générale
de la surface du cercle et la détermination de la valeur de la constante
jouant, dans la formule égyptienne, le même rôle que
p,
ce dernier aspect étant presque toujours le seul retenu.
Considérons le carré
circonscrit au cercle et construit sur son diamètre d. Comme le
carré s'étend nettement au-delà du cercle, il est clair que la surface
du carré Sp
est supérieure à la surface du cercle Sm.
Donc, le carré de surface équivalente à la surface du cercle doit avoir
un côté de longueur inférieur à celle du diamètre du cercle.
La question posée est alors
la suivante : quelle fraction du diamètre faut-il conserver pour obtenir
un carré de surface équivalente au cercle.
La réponse du mathématicien
égyptien est donnée, entre autres, dans le Problème 50 du Papyrus Rhind :
Sm
= (d-d/9)2
Cette formule appliquée par
le scribe revient à affirmer implicitement :
a)
que la surface Sm
du cercle est proportionnelle au carré de son diamètre d,
b) que le rapport
p/4
= Sm/d
a une valeur conventionnelle utilisée dans les calculs qui est (8/9)2
car on a :
Sm
= (d-d/9)2
= d2
(1-1/9) = d2
(8/9)2
C'est cette
proportionnalité qui est explicitement formulée 1000 ans plus tard par EUCLIDE
:
"Les cercles sont entre
eux comme les carrés de leurs diamètres" (Livre 12, Proposition 2,
in Les Œuvres d'Euclide, Traduction F. Peyrard, Paris,
Librairie scientifique et technique, Albert Blanchard, 1993, p. 445).
Il est important de
remarquer que la proportionnalité entre la surface et le carré du
diamètre d'un cercle et la détermination de la valeur approchée de
p
sont deux problèmes distincts.
Ainsi, outre le problème de
la proportionnalité, les Égyptiens anciens ont apporté une réponse à la
détermination numérique de
p.
En effet, la comparaison de
la formule égyptienne à la formule moderne de la surface du cercle : S =
p
d2/4
montre que le calcul du scribe revient à considérer (8/9)2
comme valeur conventionnelle de
p/4
:
S/d2
= p/4
= (8/9)2
A l'instar de la formule de
physique E = gh donnant, pour l'étalon de masse et pour
une hauteur h fixée, l'énergie potentielle (E)
avec g (intensité de la pesanteur) = 10 (dans le système
international) pour les applications numériques dans les problèmes
soumis aux étudiants, l'approximation égyptienne utilisée dans les
calculs d'application à des cas concrets revient à écrire :
p/4
= (8/9)2
= 3.16
L'écart à la valeur "exacte"
3.14 est donc d'environ 2/100.
Si l'on veut être plus
conforme à la problématique initiale on devrait écrire :
(p/4)1/2
= (8/9) d'où (p)1/2
=16/9
ce qui conduit à une
meilleure approximation : elle est de l'ordre de moins de 3/1000e
par défaut.
Le calcul présenté par le
scribe est très probablement l'application numérique et didactique d'une
formule bien connue et dûment établie.
EUCLIDE
ne dit rien sur la valeur conventionnelle ou approchée de p, dans les Œuvres qui nous sont parvenues. C'est ARCHIMÈDE
(–250 av. J.-C.) qui fera une nouvelle détermination plus précise de p
dans son traité consacré à la mesure du cercle (cf. ARCHIMÈDE,
"De la sphère et du cylindre, la mesure du cercle, sur les conoïdes
et les sphéroïdes", tome 1er, texte établi et traduit par Charles MUGLER,
Coll. des Universités de France, Paris, Les Belles Lettres, 1970).
On se propose à présent de
reconstituer un cheminement logique conduisant à la démonstration de la
formule générale de la surface du cercle — Sm
proportionnelle à d2
— en nous appuyant sur les connaissances mathématiques irréfutables des
Égyptiens, attestées par les papyrus dont nous disposons.
Considérons la figure
suivante où sont représentés deux cercles concentriques, C et C', de
rayons respectifs R et R', et discrétisés en n secteurs égaux (n
= 8, sur l'exemple de la figure ci-dessous), définissant deux polygones
réguliers à n côtés, Pn
et Pn' inscrits
respectivement dans les cercles C et C':
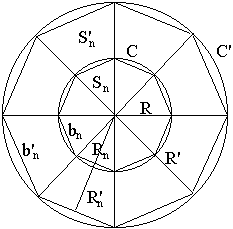
Les surfaces des
secteurs sont approximées par des triangles.
On désigne
respectivement par Sn
et Sn' les surfaces
respectives des triangles Tn
et Tn'
discrétisant les cercles C et C'. On a :
S = (1/2) bnRn
S' = (1/2) bn'Rn'
où bn
et bn' sont les bases des
triangles Tn et Tn'
et Rn et Rn'
leur hauteurs respectives. Les relations de proportionnalité entre les
côtés des triangles semblables, connues de nos jours sous le nom de
"théorème de THALÈS", mais
déjà connues des Égyptiens plus de 1000 ans avant THALÈS,
permettent d'écrire :
(bn/bn')
= (Rn/Rn')
= k
d'où
:
bn
= kRn et bn'
= kRn'
Par conséquent, les
surfaces respectives totales Sn
et Sn' des polygones Pn
et Pn'
s'écrivent :
Sn
= n (1/2) kRn2
Sn'
= n (1/2) k Rn'2
On en déduit la valeur
du rapport des surfaces Sn
et Sn'
on obtient :
Sn/Sn'
= Rn2/Rn'2
En admettant (ce qui
est conforme à l'intuition et peut être rigoureusement établi grâce
uniquement au théorème dit de THALÈS
et de son corollaire dit de PYTHAGORE)
qu'en raffinant indéfiniment la discrétisation du cercle C (resp. C'),
c'est-à-dire en augmentant indéfiniment le nombre n de côtés des
polygones Pn (resp. P'n)
considérés, la surface Sn
(resp. Sn') et la hauteur Rn
(resp R'n) du polygone de
discrétisation Pn (resp. Pn')
se rapprochent indéfiniment et respectivement de la surface S (resp. S')
et du rayon R (resp. R') du cercle C (resp. C'), par passage à la limite
sur n dans la relation précédente, on obtient la conclusion désirée :
S/S' = (R/R')2
= d2/d'2
Cette démonstration
repose donc sur la formule de la surface du triangle, le théorème de THALÈS
et la définition de la surface d'un cercle comme la limite d'un polygone
régulier inscrit lorsque le nombre de côtés devient infiniment grand.
L'ensemble de ces éléments étaient connus des Égyptiens anciens :
- la formule de la
surface d'un triangle : problème 51 du Papyrus Rhind,
problèmes 4, 7 et 17 du Papyrus de Moscou.
- l'homothétie et
le théorème de THALÈS
portant sur les triangles semblables sont attestés (cf. figure 4,
par exemple et le Problème R53 du Papyrus Rhind
reproduit sur la figure 6).
- la discrétisation en
pavés ou en secteurs est attestée (cf. figures 1, 4 et 5 par
exemple)
4. La
rectification du cercle
La
problématique de la rectification du cercle, qui est analogue à celle de
la quadrature, est la suivante :
Considérons un cercle de
diamètre d et de circonférence Cm.
On constate immédiatement que Cp
> Cm
où Cp
représente le périmètre du carré de côté égal à d exinscrit au
cercle de diamètre d. De quelle fraction faut-il diminuer le
diamètre d pour que le carré construit sur ce diamètre diminué
ait un périmètre Cp
égal à la circonférence Cm
du cercle de diamètre
d ?
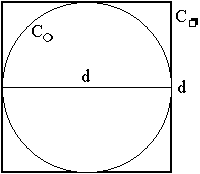
Dans les papyrus
connus à ce jour ce problème n'est pas "explicitement" traité. Cependant
on constate que dans ses onze premières lignes le Papyrus n°10 de
Moscou fournit un calcul explicite de la circonférence du cercle et
donc apporte une réponse implicite à la problématique de la
rectification du cercle.
Pour apprécier l'originalité
du papyrus égyptien, il est utile d'imaginer la manière dont un
contemporain calculerait la surface
W1/2
de la demi-sphère. Conformément à la formule moderne de la surface
W
de la sphère de diamètre d :
W
= pd2,
le mathématicien
d'aujourd'hui calculerait certainement le carré du diamètre et le
multiplierait par p/2.
On constate que le scribe
égyptien procède tout à fait autrement, en particulier, qu'il ne calcule
pas explicitement le carré du diamètre mais consacre les 11/14e
de son texte à calculer une grandeur x obtenue à la fin de la 11e
ligne avant de la multiplier par le diamètre du cercle pour obtenir le
résultat cherché. Contrairement à la démarche du mathématicien moderne,
la démarche du mathématicien égyptien ne reflète donc pas une logique
de quadrature, mais celle de l'aplanissement d'une surface
sphérique obtenue non pas comme la surface d'un carré, mais comme
celle d'un rectangle dont l'un des côtés est le diamètre et l'autre une
grandeur x calculée de manière sophistiquée :
W1/2
= xd.La question qui se pose tout naturellement est de savoir ce
que représente, dans l'esprit du scribe égyptien, pour la sphère de
diamètre d et de surface
W1/2
la grandeur x telle que
W1/2
= xd. Comme nous le montrerons plus loin, en utilisant uniquement
les connaissances mathématiques attestées par les papyrus égyptiens, on
peut aisément démontrer que
W
=
Cd où C représente la circonférence du grand cercle de la sphère.
Il est par conséquent
logique de conclure que les Égyptiens possédaient les moyens
d'interpréter x comme la demi-circonférence du grand cercle de la
sphère.
On peut affirmer avec
raison que ce papyrus fournit un calcul implicite de la circonférence
comme l'a déjà souligné STRUVE
(cité par C. A. DIOP
dans Civilisation ou Barbarie, op. cit., p. 298 : "Mais
l'exercice n° 10 nous a apporté ensemble la formule de la surface de la
sphère et celle de la longueur de la circonférence").
En examinant de près le
calcul de x donné dans le papyrus, on constate que :
x = C/2
= 2d(1-1/9)2
ce qui revient à
écrire que C = 4d(1-1/9)2
. D'après cette formule, pour les Égyptiens, la circonférence d'un
cercle de diamètre d est pratiquement équivalente au périmètre d'un
carré de côté égal au diamètre du cercle corrigé du facteur
multiplicatif (1-1/9)2.
Ceci constitue la solution pratique des Égyptiens au problème de la
rectification du cercle.
Il est naturel de se
demander comment les Égyptiens pourraient justifier rigoureusement cette
solution, en utilisant uniquement les connaissances et les méthodes
mathématiques dont ils disposaient. Les annexes 1 et 2 en fin d'article,
apportent à cette question une réponse claire et forcément technique. A
la lumière de ces réponses, on peut se convaincre que, en utilisant
seulement les connaissances mathématiques attestées par les papyrus
égyptiens, on peut démontrer que la surface S d'un cercle de
diamètre d et de circonférence C est donnée par la formule
:
S = (1/4) Cd
soit
:
C = 4 (S/d)
En utilisant la solution
égyptienne de la quadrature du cercle :
S = d2
(1-1/9)2
on en déduit la solution
égyptienne de la rectification du cercle :
C = 4d(1-1/9)2
Dans ces solutions
égyptiennes, on remarquera la simplicité de la relation entre les
cœfficients de réduction du diamètre (1-1/9)
dans le cas de la quadrature et (1-1/9)2
dans le cas de la
rectification.
Compte tenu de la
relation rappelée ci-dessus entre le diamètre d, la circonférence
C et la surface S d'un cercle, la relation que l'on peut
établir entre ces deux cœfficients revient à dire que le rapport
constant C/d est 4 fois le rapport constant S/d2,
conformément aux formules modernes : C/d =
p
et S/d2
= p/4.
5. Aplanissement de la surface de la sphère
La
solution apportée par les Égyptiens peut être exprimée de la manière
suivante : la surface de la 1/2 sphère est égale à celle du rectangle
dont un côté est le diamètre de la sphère et l'autre la
demi-circonférence du grand cercle. Cette surface se trouve être égale à
celle de la paroi droite d'un cylindre tangent à la sphère et dont la
hauteur est égale à la hauteur de la 1/2 sphère.
Pour apprécier la pertinence
de la problématique de l'aplanissement d'une surface courbe, considérons
le problème concret suivant :
Étant donnée l'écorce d'une
demi-orange dont on cherche à évaluer la surface en la ramenant à une
surface plane on se rend compte d'une part que l'on ne peut pas
l'aplanir sans la déchirer et en second lieu on se demande à quelle
surface plane simple elle peut bien être équivalente ? Par ailleurs, si
l'on considère la moitié d'un quartier d'écorce que l'on aplanit, on
s'aperçoit que la surface aplanie n'est pas un triangle mais a plutôt la
forme d'un fer à repasser dont on se demande bien comment déterminer la
surface.
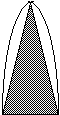
En termes
mathématiques précis, la problématique de l'aplanissement de la sphère
est la suivante :
Étant donnée une sphère de
surface S et de diamètre d, quels sont les côtés d'un rectangle de
surface équivalente à S. Cette problématique apparaît clairement dans la
démarche du scribe égyptien qui obtient à la fin de son calcul la
surface de la sphère non pas comme la surface d'un carré, mais comme
celle d'un rectangle dont l'un des côtés est le demi-diamètre (d/2)
et l'autre la circonférence du grand cercle (C) comme nous
l'avons exposé au paragraphe §4 consacré à la rectification du cercle.
La solution magistrale apportée par les Égyptiens à ce problème est la
suivante :
La surface
S d'une
sphère de diamètre d et de grand cercle de circonférence C
est égale à celle du rectangle construit sur le diamètre et dont l'autre
côté est obtenu en dépliant le grand cercle de la sphère.
Puisque cette surface se
trouve être aussi égale à celle de la paroi droite du cylindre exinscrit
à la sphère et de hauteur le diamètre, on a S = Cd.
D'après la relation interne existant entre les éléments caractéristiques
d'un cercle, on en déduit trivialement que la surface de la sphère est
égale au quadruple de celle de son grand cercle, et aux 2/3 de la
surface totale (paroi et bases) du cylindre exinscrit à la sphère. On
retrouve ainsi une partie des résultats laborieusement retrouvés par ARCHIMÈDE
et qui l'ont enthousiasmé au point de demander à en graver la
représentation sur sa tombe, et au sujet desquels il écrivait avec
exaltation à son ami DOSITHÉ.
7. Conclusion
Tirant
toutes les conséquences des faits mathématiques égyptiens se rapportant
au calcul de la surface du cercle et de celle de la demi-sphère
respectivement exposés dans le Papyrus Rhind et le Papyrus de
Moscou nous avons abouti aux conclusions suivantes :
— la propriété du rapport
constant entre la surface d'un cercle et son diamètre est connue des
Égyptiens et il s'agit d'une problématique distincte de celle de la
quadrature qui vise à déterminer l'équivalent égyptien du facteur p pour
approximer la surface d'un cercle par celle d'un carré.
— l'étude conjointe des
problèmes relatifs au calcul de la surface du cercle et de la surface
d'une demi-sphère montre que les relations internes entre les
caractéristiques d'un cercle sont connues des Égyptiens.
— Les formules de
calcul de la surface du cercle et de la demi-sphère, telles qu'elles
apparaissent — c'est-à-dire générales et exactes — dans le Papyrus
Rhind et le Papyrus de Moscou, supposent l'introduction de la
notion de mesure au sens mathématique du mot que le mathématicien
Égyptien a su rendre opératoire.
Plus généralement, les
papyrus mathématiques égyptiens, et en particulier le Papyrus Rhind,
dont le titre est : "Méthode correcte d'investigation dans la
nature pour connaître tout ce qui existe, chaque mystère, tous les
secrets" [T. OBENGA,
La Géométrie égyptienne, op. cit., p. 290], témoignent de
cette conquête de la raison humaine : l'homme découvre qu'il peut
accéder à la connaissance du réel grâce à des formules mathématiques. Les formes idéales que sont le cercle, le rectangle, le carré,
l'ellipse, la pyramide, etc., n'existent nullement dans la nature.
L'Égyptien a su concevoir ces formes idéales, reconnaître les propriétés
géométriques qui leur sont intrinsèquement attachées, indépendamment de
leurs dimensions, traduire ces propriétés en termes de formules
mathématiques. L'Égyptien, dans un retour vers le réel, utilise les
propriétés ainsi reconnues et les formules mathématiques associées pour
résoudre des problèmes concrets : architecture, économie, agriculture,
astronomie, etc. A cette fin, le mathématicien met au point des
algorithmes de calculs et des conventions numériques qui suffisent à ses
exigences de précision.
La découverte de
la possibilité de connaître la Nature au moyen d'une formulation
mathématique constitue un événement majeur dans l'histoire de la pensée
scientifique. En Afrique, cette découverte semble s'être faite au
travers de la géométrie, c'est-à-dire de la mesure de la terre
étymologiquement parlant, en raison de la configuration géo-climatique
particulière de la vallée du Nil, en Égypte même. Les Égyptiens ont
puissamment contribuer à ouvrir la voie de la connaissance scientifique
du réel, celle qu'ont empruntée à leur suite les Grecs, celle que
continue d'emprunter le chercheur d'aujourd'hui. Kenneth G. WILSON,
professeur de physique à l'Université Cornell aux USA (Ithaca, New
York), lauréat du Prix Nobel de Physique 1982, au détour d'une réflexion
prospective relative aux ordinateurs, rappelle l'origine égyptienne de
l'investigation théorique :
"Les superordinateurs
conduiront à la mise en œuvre, dans le domaine de la recherche
scientifique, d'une stratégie inédite, résolument novatrice, appelée à
s'inscrire à la suite de l'approche théorique inaugurée par l'ancienne
Égypte, et des techniques expérimentales remontant à l'époque de
Galilée."
C'est cette
découverte égyptienne qui a frappé l'esprit des anciens Grecs venus
s'initier en Égypte. Les problèmes posés et résolus par les anciens
Égyptiens pour la première dans l'histoire de la mathématique
universelle seront repris, plus de mille ans après qu'ils aient été
énoncés, par les Grecs de l'époque classique (THALÈS,
PYTHAGORE, ...) puis ceux de
l'époque hellénistique, en particulier EUCLIDE,
qui a passé sa vie en Égypte et qui est l'auteur de traités de
Géométrie, ARCHIMÈDE de
Syracuse, qui a fait ses découvertes postérieurement à son séjour en
Égypte. ARCHIMÈDE est
l'auteur d'un ouvrage intitulé De la sphère et du cylindre, la mesure
du cercle, sur les conoïdes et les sphéroïdes dans lequel il établit
la relation interne existant entre les éléments caractéristiques d'un
cercle et démontre que "Le périmètre de tout cercle est égal au
triple du diamètre augmenté d'un segment compris entre les dix soixante
et onzièmes et le septième du diamètre", ce qui est équivalent à
l'évaluation d'une nouvelle valeur du nombre p. A propos de l'ensemble
de ses travaux sur la sphère et le cylindre, ARCHIMÈDE
écrit à son ami DOSITHÉE : "Ces
propriétés préexistaient, liées à la nature des figures indiquées, mais
elles étaient ignorées de ceux qui se sont occupés de la géométrie avant
nous, personne d'entre eux ne s'étant aperçu que les mesures de ces
figures sont comparables" (De la sphère et du cylindre, la mesure
du cercle, sur les conoïdes et les sphéroïdes, Livre I, "ARCHIMÈDE
à DOSITHÉE,
joie !").
Le travail présenté
ci-dessus s'inscrit dans la perspective d'une ré-écriture de l'histoire
des sciences qui restituera le véritable apport de l'Afrique à
l'humanité dans le domaine particulier des sciences exactes.
Cette tâche oblige le
chercheur à reprendre l'étude approfondie des textes égyptiens sans
préjugés idéologiques. C'est pour cette raison qu'il faut attirer
l'attention sur le fait que l'approche courante qui postule le caractère
empirique et strictement utilitaire des mathématiques égyptiennes,
considérées dès lors comme un ensemble de recettes, se heurte à de
graves faiblesses méthodologiques :
— Elle oppose, en effet, de
manière tout à fait arbitraire et artificielle la démarche empirique et
l'étape de théorisation qui opère à partir d'observations, d'échecs et
de réussites constatés. Des formules exactes et générales ne peuvent
être établies qu'à partir d'une démarche à caractère abstrait qui se
détache du problème particulier à résoudre. Or, les Égyptiens anciens
ont établi de telles formules comme en témoignent les papyrus
mathématiques connus.
— Une telle démarche
tente également de minimiser l'ampleur de l'héritage égyptien dans la
pensée grecque, et ce, en totale contradiction avec le témoignage
unanime des savants grecs eux-mêmes. Ce faisant, elle empêche de cerner
les conditions réelles de la naissance de la science et de son
développement dans le monde gréco-latin. Elle tend, en effet, à
substituer à l'explication historique rationnelle et vérifiable la
génération spontanée de la connaissance incarnée par le concept
irrationnel du "miracle grec" contre lequel s'élevait déjà avec
vigueur le père de l'Égyptologie,
Jean-François CHAMPOLLION
:
"Une étude
sérieuse, dégagée du préjugé vulgaire qui, malgré l'évidence des faits
et le témoignage positif des anciens Grecs eux-mêmes, tendrait à faire
admettre le système de la génération spontanée des arts, des sciences et
de toutes les institutions sociales sur le sol de l'ancienne Grèce, nous
démontre que, comme partout ailleurs peut-être, ce pays, habité d'abord
par quelques hordes barbares, fut successivement occupé aussi par des
populations étrangères dont l'arrivée opéra de grands changements …"
(Discours d'ouverture du cours d'archéologie au Collège Royal de
France, le 10 mai 1831 in Jean-François CHAMPOLLION,
Principes généraux de l'écriture sacrée égyptienne, Paris,
Institut d'Orient, 1984, p. v).
Plus loin dans le même
Discours (p. xxij et xxiij) on lit :
"L'interprétation des
monuments de l'Égypte mettra encore mieux en évidence l'origine
égyptienne des sciences et des principales doctrines philosophiques de
la Grèce ; l'école platonicienne n'est que de l'égyptianisme, sorti des
sanctuaires de Saïs …"
— Enfin, cette approche
conduit à des problèmes d'interprétation insurmontables, par la
recherche de méthodes empiriques introuvables, mystérieuses, qui
expliqueraient les formules exactes égyptiennes. Elle interdit dès lors
l'accès à des interprétations mathématiques parfaitement compatibles
avec le niveau de connaissance tel qu'il est attesté dans les documents
disponibles.
Prendre la véritable mesure
de la science égyptienne et de son impact profond sur le monde
intellectuel de l'Antiquité c'est contribuer à l'intelligibilité de
l'histoire des idées de cette période. La perspective historique et
géographique avec laquelle les faits relatifs au développement de la
science dans l'Antiquité doivent être appréhendés, permettra de mieux
caractériser l'apport de l'Afrique à la science tout en évitant de
substituer à un miracle grec, un miracle africain.
Notes
1.
Eric, T. PEET, The Rhind Mathematical Papyrus, The University
Press of Liverpool, 1923 ; "A problem in Egyptian Geometry", in
JEA, tome 17, 1931 ; Otto NEUGEBAUER, The Exact Science in
Antiquity, New York, Harper, 1962 ; V. V. STRUVE, Mathematischer
Papyrus des Staatlichen Museums der Schönen Künste in Moskau, Quellen
und Studien zur Geschichte der Mathematik, Abt. A, Quellen, Band I,
Berlin, 1930 ; R. J. GILLINGS, Mathematics in the Time of the
Pharaohs, New York, Dover Publications, Inc., 1982 (1ère édition
1972), Cheikh Anta DIOP, Civilisation ou Barbarie, Paris,
Présence africaine, 1981 ; Théophile OBENGA, La philosophie africaine
de la période pharaonique, Paris, L'Harmattan, 1990., Théophile
OBENGA, La Géométrie égyptienne - Contribution de l'Afrique antique à
la Mathématique mondiale, Paris, L'Harmattan/Khepera, 1995 ; Sylvia
COUCHOUD, Mathématiques égyptiennes, Recherches sur les connaissances
mathématiques de l'Égypte pharaonique, Paris, Éditions Le Léopard
d'Or, 1993.
2.
Cf. André P. R. POCHAN, Les Calendriers des Anciens Égyptiens,
Montesson, Édition de Maât, 1962 ; Cheikh Anta DIOP, Civilisation ou
Barbarie, Paris, Présence africaine, 1981 ; Théophile OBENGA, La
philosophie africaine de la période pharaonique, Paris, L'Harmattan,
1990.
3. Cf. W.
F. PETRIE, Ancient Weights and Measures, Londres, 1926 ; Karl M.
PETRUSO, "Early Weights and Weightings in Egypt and the Indus Valley",
in Bulletin of the Museum of Fine Arts, 79, 1981, p. 44-51
; Marguerite-Annie COURT-MARTY, "Les poids égyptiens, de précieux
jalons archéologiques", in CRIPEL 12, 1990, pp. 17-55,
"Les poids et la pesée dans l'Égypte ancienne", in
Cahiers de Métrologie, tomes 11-12, 1993-1994, pp. 345-358.
4.
Cf. Cheikh Anta DIOP, op. cit. ; Théophile OBENGA, La
Géométrie égyptienne - Contribution de l'Afrique antique à la
Mathématique mondiale, Paris, L'Harmattan/Khepera, 1995 ; Sylvia
COUCHOUD, Mathématiques égyptiennes, Recherches sur les connaissances
mathématiques de l'Égypte pharaonique, Paris, Éditions Le Léopard
d'Or, 1993.
5.
L'établissement de la formule donnant la surface du rectangle, telle que
nous l'avons exposée ci-dessus, permet de saisir pourquoi les Grecs
anciens, formés en Égypte pharaonique, "parlaient du rectangle de
deux segments pour qualifier le produit de deux nombres" (Géométrie,
Encyclopaedia Universalis).
6.
Théophile OBENGA, La Géométrie égyptienne - Contribution de l'Afrique
antique à la Mathématique mondiale, op. cit.
7.
R. J. GILLINGS, Mathematics in the Time of the Pharaohs, New
York, Dover Publications, Inc., 1982 (1ère édition 1972).
8.
EUCLIDE, comme la plupart des savants grecs, a séjourné à Alexandrie, en
Égypte, où il a fondé (IIIe siècle av. J.-C.) une école mathématique.
9.
Il est frappant de constater que les différentes branches des
mathématiques, en Occident, ont gardép jusqu'au siècle dernier la
mémoire de leur origine géométrique égyptienne : "Jusqu'au début des
Temps modernes, presque toute la mathématique s'exprimait
géométriquement : ainsi la Géométrie de Descartes traite non
seulement de géométrie, mais aussi des équations algébriques. Et, au
XIXe siècle, les mathématiciens étaient encore bien souvent qualifiés de
géomètres, même quand ils étaient de purs analystes ou algébristes."
(Géométrie, Encyclopaedia Universalis).

